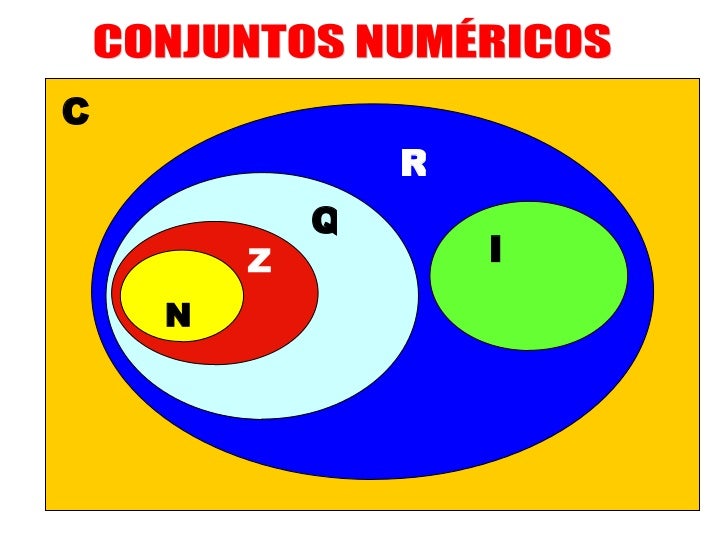
CONJUNTOS NUMÉRICOS:
NÚMEROS NATURALES: son aquellos números que se utilizan para contar. Por ejemplo: 1, 2, 3, 4, etc. Se representan con la letra N.
NÚMEROS ENTEROS: son todos los números naturales más el cero y los números negativos. Se representan con la letra Z.
NÚMEROS RACIONALES: incluyen fracciones y números decimales. Por ejemplo: 1,5, 1/2, etc. Se representan con la letra Q.
NÚMEROS IRRACIONALES: son todos aquellos números con decimales infinitos no periódicos. Por ejemplo el número Pi. Se representan con la letra I.
NÚMEROS REALES: están integrados por el conjunto de los números racionales e irracionales. Se representan con la letra R.
----------------------------------------------------------------------------------------------------------------------------
SUCESIONES:
Los términos de una sucesión siguen una regularidad que la caracteriza.
Ejemplo:
----------------------------------------------------------------------------------------------------------------------------
SUCESIONES:
Los términos de una sucesión siguen una regularidad que la caracteriza.
Ejemplo:
- Dada la siguiente sucesión: an= (1+1/n)^2 - Determinar cuáles son los primeros 10 términos de la sucesión. ¿Cuánto vale a100 y cuánto vale a1000?
a1= 2 a6= 2,521 a100= 2,704
a2= 2,25 a7= 2,546 a1000= 2,716
a3= 2,370 a8= 2,565
a4= 2,441 a9= 2,581
a5= 2,488 a10= 2,593
Video explicativo de sucesiones numéricas:
-----------------------------------------------------------------------------------------------------------------------------
VALOR ABSOLUTO:
El valor absoluto se utiliza para nombrar el valor que tiene un número más allá de su signo, es decir, la distancia que hay entre este número y el cero.
Ejemplo: |-3| = 3
| 5| = 5
Más información sobre el valor absoluto:
http://www.profesorenlinea.cl/matematica/Valor_absoluto.html
------------------------------------------------------------------------------------------------------------------------------
INTÉRVALOS:
Cuando el intervalo se representa con un corchete significa que se trata de un intervalo cerrado. Cuando se representa con un paréntesis significa que se trata de un intervalo abierto.
- Intervalo expresado en términos de desigualdad: 2<X<8
- Intervalo expresado en notación de intervalo: [2;8)
---------------------------------------------------------------------------------------------------------------------------------
Video explicativo de sucesiones numéricas:
-----------------------------------------------------------------------------------------------------------------------------
VALOR ABSOLUTO:
El valor absoluto se utiliza para nombrar el valor que tiene un número más allá de su signo, es decir, la distancia que hay entre este número y el cero.
Ejemplo: |-3| = 3
| 5| = 5
Más información sobre el valor absoluto:
http://www.profesorenlinea.cl/matematica/Valor_absoluto.html
------------------------------------------------------------------------------------------------------------------------------
INTÉRVALOS:
Cuando el intervalo se representa con un corchete significa que se trata de un intervalo cerrado. Cuando se representa con un paréntesis significa que se trata de un intervalo abierto.
- Intervalo expresado en términos de desigualdad: 2<X<8
- Intervalo expresado en notación de intervalo: [2;8)
---------------------------------------------------------------------------------------------------------------------------------
FUNCIONES LINEALES:
El modelo de una función lineal es el siguiente: f(x)= ax+b
Reciben ese nombre porque al ser graficadas se obtienen rectas. Todas las funciones lineales tienen dominio e imagen en el campo de los números reales.
En una función lineal, el valor de "a" influye en la inclinación de la pendiente, mientras que el valor de "b" va a determinar la distancia entre el cero y el corte del eje Y.
Ejemplo:
FUNCIONES CUADRÁTICAS:
El modelo de una función cuadrática es el siguiente: ax^2+bx+c
Recibe su nombre porque la X se encuentra elevada al cuadrado. El dominio y la imagen de toda función cuadrática se encuentra en el campo de los números reales.
El término "a" determina si las ramas de la parábola van a ir hacia arriba o hacia abajo, dependiendo si este es positivo o negativo.
Ejemplo:
El modelo de una función lineal es el siguiente: f(x)= ax+b
Reciben ese nombre porque al ser graficadas se obtienen rectas. Todas las funciones lineales tienen dominio e imagen en el campo de los números reales.
En una función lineal, el valor de "a" influye en la inclinación de la pendiente, mientras que el valor de "b" va a determinar la distancia entre el cero y el corte del eje Y.
Ejemplo:
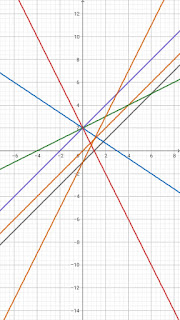
Representación gráfica de las siguientes funciones lineales:
f(x)= x
f(x)= x+2
f(x)= x-1
f(x)= 1/2x+2
f(x)= -2/3x+2
f(x)= -2x+2
f(x)= 2x-1
FUNCIONES CUADRÁTICAS:
El modelo de una función cuadrática es el siguiente: ax^2+bx+c
Recibe su nombre porque la X se encuentra elevada al cuadrado. El dominio y la imagen de toda función cuadrática se encuentra en el campo de los números reales.
El término "a" determina si las ramas de la parábola van a ir hacia arriba o hacia abajo, dependiendo si este es positivo o negativo.
Ejemplo:
Representación gráfica de las siguientes funciones:
f(x)= x^2
f(x)= x^2+1
f(x)= x^2-1
f(x)= 2x^2
f(x)= -x^2
Para calcular el vértice de una función cuadrática: -b
Xv= --------
2.a
f(x)= x^2
f(x)= x^2+1
f(x)= x^2-1
f(x)= 2x^2
f(x)= -x^2
Para calcular el vértice de una función cuadrática: -b
Xv= --------
2.a
No hay comentarios.:
Publicar un comentario